Appendix1.1 Hypothetical application 1

II . HYPOTHETICAL APPLICATION 1

note:
The first hypothetical application (description1) includes and the second (description2) does not include underlined written description.

CURVE GENERATING METHOD USING
TANGENT VECTORS

BACKGROUND OF THE INVENTION

1. Field of the Invention

This invention relates to a curve generating method and, more particularly, to a method of generating a three-dimensional curved surface.

2. Description of the Related Art

A curved surface of a three-dimensional metal mold or the like on a design drawing is generally expressed by a plurality of section curves, but no profile data is shown for the shape of the area lying between a certain section curve and the next adjacent section curve. In numerically controlled machining it is essential that machining be carried out so as to smoothly connect these two section curves despite the next adjacent section curve. In numerically controlled machining it is essential that machining be carried out so as to smoothly connect these two section curves despite the fact that the profile between them is not given. In other words, this means that machining must be performed by generating the curved surface between the two section curves from such data as that indicative of the section curves, recording on an NC tape the data concerning the generated curved surface, and carrying out machining in accordance with commands from the NC tape. To this end, there has been proposed a method of generating the curved surface of a three-dimensional curved body in accordance with predetermined rules using data(e.g. section curves and the like) specifying the three-dimensional curved body.
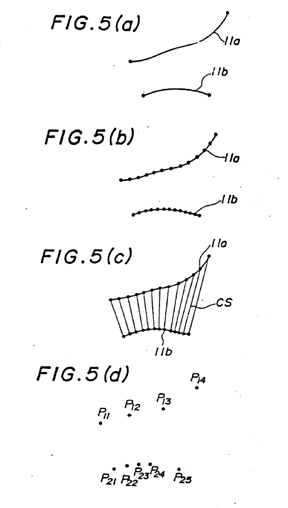
FIGS.5(a)-(b) for describing a curved surface generating method, in which a curved surface CS [see FIG.5(c)] is generated by providing three-dimensional curves (reference curves) 11a, 11b [see FIG.5(a)] of a curved surface cut by a predetermined section, dividing each of the reference curves 11a, 11b into N equal segments [see FIG.5(b)], and connecting corresponding ones of the partitioning points by straight lines.
In this curved surface generating method, the reference curves 11a, 11b, which are the three-dimensional curves, must be specified. To this end, a sequence of discrete point P1i (xi,yi,zi) (i = 1,2,...) is given with regard to the reference curve 11a, as shown in FIG.5(b), a sequence of discrete points P2j (Xi, Yi, Zi) (j = 1,2,...) is given with regard to the reference curve 11b, and curves (reference curves) connecting these point sequences are obtained by performing interpolation between points so as to smoothly connect the respective point sequences.
In this conventional method of generating the point sequence connecting curves, it is necessary to determine a tangent vector at each point. However, the method of determining these tangent vector is a major undertaking requiring matrix computations, inverse matrix computations, etc., and it is impossible for an ordinary curved surface generating apparatus on the personal computer level to determine the tangent vectors.

SUMMARY OF THE INVENTION

Accordingly, an object of the present invention is to provide a curve generating method trough which tangent vector can be determined in a simple manner, thus making it possible to simply obtain curves smoothly connecting point sequences.
The method of the present invention includes determining a circular arc passing through three discretely given consecutive points Pi-1, Pi, Pi+1, determining a tangent vector of a tangent line contacting the circular arc at the central point Pi of these three points, thereafter performing a spline interpolation between the two points Pi-1, Pi, using position vectors and tangent vectors at the points Pi-1, Pi, thereby obtaining a curve smoothly connecting the two points Pi-1, Pi, and thereafter determining a point sequence connecting curve by similarly performing an interpolation between every two consecutive points discretely given.

BRIEF DESCRIPTION OF THE DRAWINGS

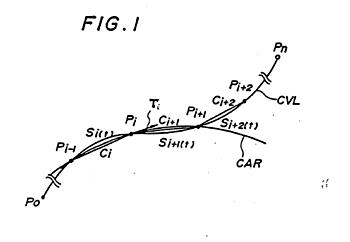
• FIG.1 is a view for describing the general features of the present invention;
  
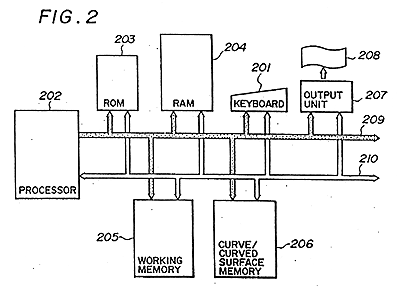
• FIG.2 is a block diagram of an apparatus for practicing the present invention;
  
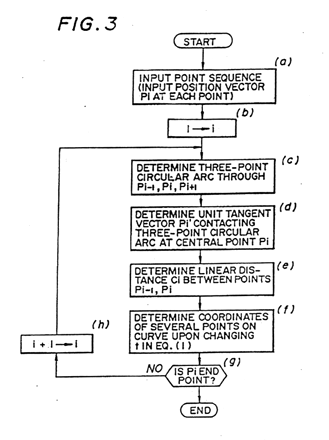
• FIG.3 is a flowchart of processing according to the present invention;
  
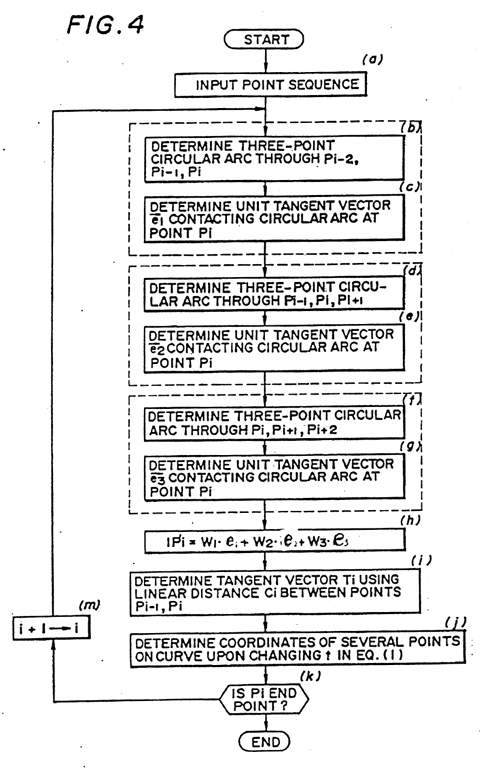
• FIG.4 is a flowchart of different processing according to the present invention.
  
• FIG.5(a) - 5(d) for describing a method of generating a curved surface.

DETAILED DESCRIPTION OF THE PREFERRED EMBODIMENT

FIG.1 is a view for describing the general features of the present invention.
Pi(i = 1,2,... n) represents a sequence of points, CVL a curve smoothly connecting the sequence of points, CAR a circular arc passing through three consecutive points, Ci the linear distance between adjacent points, and Si(t) the coordinates of a point on the curve CVL.
The circular arc CAR passing through three discretely given consecutive points Pi-1, Ri, Ri+1 is determined, followed by determining a tangent vector Ti of tangent contacting the circular arc at the central point Pi.
A tangent vector Ti-1 at the point Pi-1 is then found in similar fashion.
Next, by using position vectors Pi-1, Pi and tangent vector Ti-1,Ti at the points Pi-1, Pi, a spline interpolation is performed between Pi-1, Pi to obtain the coordinates Si(t) (where is a value increased at increments of 0.1 from 0 to 1), and a curve which smoothly connects the two points Pi, Pi+1 is determined.
Thereafter, and in similar fashion, the point sequence connection curve CVL is obtained by performing an interpolation between every two consecutive points of the discretely given points of the discretely given points. Fig.2 is a block diagram of an embodiment of the invention, and FIG.3 is a flowchart of processing. In FIG.2, numeral 201 denotes a keyboard for data input, 202 a RAM, 205 a working memory, 206 a curve/curved surface memory for storing generated curve and curved surface data, 207 an output unit for outputting generated curved surface data to an external storage medium 208 such as a paper tape or magnetic tape, 209 an address bus and 210 a data bus.
Processing for generating a curve in accordance with the invention will now be described in accordance with the flowchart of FIG.3.

(a) First, data specifying a three-dimensional curved surface, e.g. a point sequence (a position vector Pi at each point) specifying the curve CVL (FIG.1), is inputted from the keyboard 201.

(b) Next, the processor performs the operation 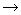1 1.

(c) Thereafter, the circular arc CAR (see FIG.1) passing through the discretely given three consecutive points Pi-1, Pi, Pi+1 is found.

(d) When the circular arc CAR has been found, a unit tangent vector Pi of a tangent line contacting the circular arc CAR at the central point Pi is obtained.

(e) Next, the linear distance Ci between the point Pi-1 and the pint Pi is computed.

(f) When the distance Ci has been found, the coordinates Si(t) of points on the curve smoothly connecting the point Pi-1, Pi pare computed by varying t over a range of from 0 to 1, namely by performing spline interpolation, in accordance with the following equation;

In Eq. (1), Si(t) represents the coordinates of point Pi-1 if t=0 the coordinates of point Pi if t=0.5. Accordingly, nine points between points Pi-1, Pi are obtained by incrementing at 0.1, interpolation is performed over this interval, and the coordinates of each point are stored in the memory 206. It should be noted that Eq. (1) is an induction equation of a Ferguson curve segment.

(g) Next, it is determined whether the point Pi is the end point of the curve. If Pi is the end point, & curve generation processing is terminated.

(h) If the point Pi is not the end point of the curve, however, i is incremented by the operation i+1 i and processing is repeated from step(c) onward to perform interpolation between every two consecutive points discretely given, whereby a point sequence connecting curve is obtained. The processing of FIG.3 is for a case where a tangent vector is found using three consecutive points. However, a tangent vector can also be obtained by using five consecutive points. FIG.4 is a flowchart for obtaining a tangent vector using five points, and obtaining a curve using the tangent vector.

(a) First, data specifying a three-dimensional curved surface, e.g. a point sequence (a position vector Pi at each point) specifying a curve is inputted from the
keyboard 201.

(b) Thereafter, a circular arc passing through three discretely given consecutive point Pi-2, Pi-1, Pi is found.

(c) When the circular arc has been found, a unit tangent vector ej of a tangent line contacting the circular arc at a point Pi at the right end is obtained.

(d) Next, a circular arc passing through the three discretely given consecutive points Pi-1, Pi, Pi+1 is found.

(e) When the circular arc has been found, a unit tangent vector e2 of a tangent line contacting the circular arc at the central point Pi is obtained.

(f) Next, a circular arc passing through the three discretely given consecutive points Pi, Pi+1 Pi+2 is found.

(g) When the circular arc has been found, a unit tangent vector e3 of a tangent line contacting the circular arc at a point Pi at the left end is obtained.

(h) When the unit tangent vector e1 - e3 have been obtained, a unit tangent vector Pi' at the point Pi is found in accordance with the following equation:

Pi' = w1e1 + w2e2 + w3e3

In the above wi(i=1,2,3) is a weighting coefficient obtained in accordance with the following equation so that the unit tangent vector where the interval between points is small will be reflected in the curve:

• w1=1-(Ci+Ci-1)/(Ci-1+2Ci+2Ci+1+Ci+2)
• w2=1-(Ci+Ci+1)/(Ci-1+2Ci+2Ci+1+Ci+2)
• w3=1-(Ci+1+Ci+2)/(Ci-1+2Ci+2Ci+1+Ci+2)

where the distance between points Pi-2, Pi-1 is Ci-1, the distance between point Pi-1, Pi is Ci, the distance between points Pi, Pi+1 is Ci+1 and the distance between points Pi+1, Pi+2 is Ci+2.

(i) Next, the tangent vector Ti is computed in accordance with the equation

Ti=CiPi'

using the linear distance Ci between the point Pi-1and the point Pi.

(j) This is followed by varying t over the range of from 0 to 1 in accordance with Eq.(1) to compute the coordinates Si(t) of points on the curve smoothly connecting the points Pi-1, Pi.

(k) Next,it is determined whether the point Pi is the end point of the curve. If Pi is the end point, curve generation processing is terminated.

(m) If the point Pi is not the end point of the curve, however, is incremented by the operation i+1 i and processing is repeated from step (b) onward to perform interpolation between every two consecutive points discretely given, whereby a point sequence connecting curve is obtained.

In accordance with the present invention, the arrangement is such that a tangent vector at each point of a point sequence is obtained by using three or five consecutive points. As a result, tangent vectors can be obtained in a simple manner and, hence, a curve smoothly connecting the point sequence can be obtained in simple fashion.
With the method of obtaining tangent vectors in accordance with Eq.(2) using five points, a curve can be minutely altered by changing the manner in which each weighting coefficient is decided, thereby making it possible to generate the desired curve.

We claim :

1. A method of generating a curve comprising the steps of:

• (a) detecting a circular arc passing through three discretely given consecutive points Pi-1, Pi, Pi+1 of the curved surface.
  
• (b) determining a tangent vector of a tangent line contacting said circular arc at the central point Pi of said three points;
  
• (c) determining a curve smoothly connecting the two points Pi-1, Pi by performing a spline interpolation between the two points Pi-1, Pi using position vectors Pi-1, Pi at the points Pi-1, Pi and tangent vectors Ti-1, Ti at the points Pi-1, Pi determined in step(b);
  
• (d) determining a point sequence connecting curve by performing a spline interpolation between every two adjacent consecutive points

2. A method of generating a curve by computer comprising the steps of:

• (a) detecting a circular arc passing through three discretely given consecutive points Pi-1, Pi, Pi+1 of the curved surface.
  
• (b) determining a tangent vector of a tangent line contacting said circular arc at the central point Pi of said three points;
  
• (c) determining a curve smoothly connecting the two points Pi-1, Pi by performing a spline interpolation between the two points Pi-1, Pi using position vectors Pi-1, Pi at the points Pi-1, Pi and tangent vectors Ti-1, Ti at the points Pi-1, Pi determined in step(b);
  
• (d) determining a point sequence connecting curve by performing a spline interpolation between every two adjacent consecutive points.

3. A method of machining a three-dimensional curved surface comprising the steps of:

• (a) detecting a circular arc passing through three discretely given consecutive points Pi-1, Pi, Pi+1 of the curved surface.
  
• (b) determining a tangent vector of a tangent line contacting said circular arc at the central point Pi of said three points;
  
• (c) determining a curve smoothly connecting the two points Pi-1, Pi by performing a spline interpolation between the two points Pi-1, Pi using position vectors Pi-1, Pi at the points Pi-1, Pi and tangent vectors Ti-1, Ti at the points Pi-1, Pi determined in step(b);
  
• (d) determining a point sequence connecting curve by performing a spline interpolation between every two adjacent consecutive points; and
  machining the three-dimensional curved surface according to the point sequence connecting curve.

4. A method of generating a curve for machining a three-dimensional curved surface comprising the steps of:

• (a) detecting a circular arc passing through three discretely given consecutive points Pi-1, Pi, Pi+1 of the curved surface.
  
• (b) determining a tangent vector of a tangent line contacting said circular arc at the central point Pi of said three points;
  
• (c) determining a curve smoothly connecting the two points Pi-1, Pi by performing a spline interpolation between the two points Pi-1, Pi using position vectors Pi-1, Pi at the points Pi-1, Pi and tangent vectors Ti-1, Ti at the points Pi-1, Pi determined in step(b);
  
• (d) determining a point sequence connecting curve by performing a spline interpolation between every two adjacent consecutive points;

5. A method of displaying a generated curve by computer comprising the steps of:

• (a) detecting a circular arc passing through three discretely given consecutive points Pi-1, Pi, Pi+1 of the curved surface.
  
• (b) determining a tangent vector of a tangent line contacting said circular arc at the central point Pi of said three points;
  
• (c) determining a curve smoothly connecting the two points Pi-1, Pi by performing a spline interpolation between the two points Pi-1, Pi using position vectors Pi-1, Pi at the points Pi-1, Pi and tangent vectors Ti-1, Ti at the points Pi-1, Pi determined in step(b);
  
• (d) determining a point sequence connecting curve by performing a spline interpolation between every two adjacent consecutive points; and
  displaying the three-dimensional curved surface according to the point sequence connecting curve.

6.A method of controlling a curve generating apparatus including a keyboard for data input, a processor, a ROM for storing a control program, a RAM, a working memory, an output unit for outputting generated curved surface data to an external storage medium, an address bus and a data bus, said control program comprising the steps of

• (a) detecting a circular arc passing through three discretely given consecutive points Pi-1, Pi, Pi+1 of the curved surface.
  
• (b) determining a tangent vector of a tangent line contacting said circular arc at the central point Pi of said three points;
  
• (c) determining a curve smoothly connecting the two points Pi-1, Pi by performing a spline interpolation between the two points Pi-1, Pi using position vectors Pi-1, Pi at the points Pi-1, Pi and tangent vectors Ti-1, Ti at the points Pi-1, Pi determined in step(b);
  
• (d) determining a point sequence connecting curve by performing a spline interpolation between every two adjacent consecutive points.

III . HYPOTHETICAL PRIOR ART

HYPOTHETICAL PRIOR ART NO.1

Only induction equation of a Ferguson curve segment is disclosed in the hypothetical prior art.

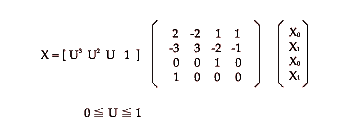
HYPOTHETICAL PRIOR ART NO.2

COMPUTER GRAPHICS AND IMAGE PROCESSING VOL.11, 1979,PAGES 192-196, ACADEMIC PRESS INC., NEW YORK,US; J.E. MIDGLEY: "ISOTROPIC FOUR-POINT INTERPOLATION"